重力異常について（解説）

１．重力異常と密度構造
　地球重力場は地球の全質量があたかも地球の中心に集中しているかのような成 分に地球の自転による遠心力の成分が合成された標準的な重力場(980 gal 程度)と，地下構造による 密度の不均質性から生ずる擾乱場からなる．後者を重力異常(大きくても数10mgal程度) という．なお，gal（ガル という表記については，ガリレオ・ガリレイに因むが，SI 単位でないため表記については特に決 まりはなく，Gal と表記されることもある． 標準的な重力場は，密度構造が緯度・経度方向には変化を伴わず半径方向だけに 変化を伴う重力効果（引力）と地球の自転による遠心力が合成された標準モデルの重力である．重力異常は，その標 準モデルからずれた不均質の密度構造から生じているものである．つまり，この重力異常（観測値） を求めれば，その観測値を説明する不均質構造を得ることができる．重力探査の対象となる模式的 な地殻構造を付図1 に示す．

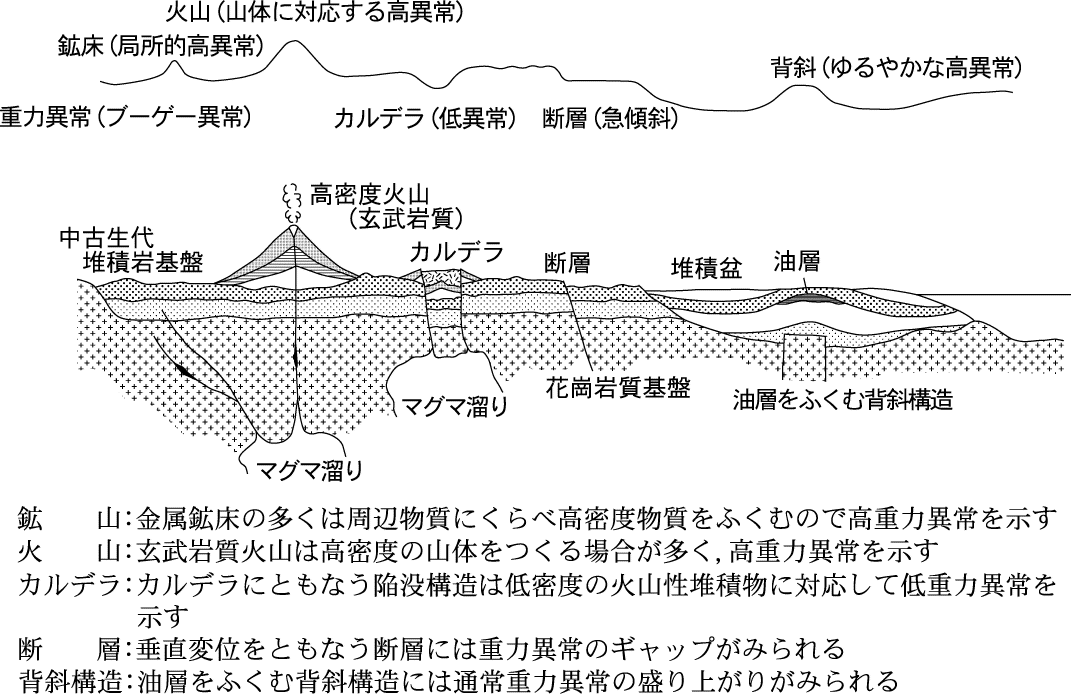
付図1 地殻構造と重力異常の概念図（物理探査学会編，1989 に加筆修正）


２．ブーゲー異常の算出と物理的な意味
　ブーゲー異常の算出過程を付図2に従って説明する．

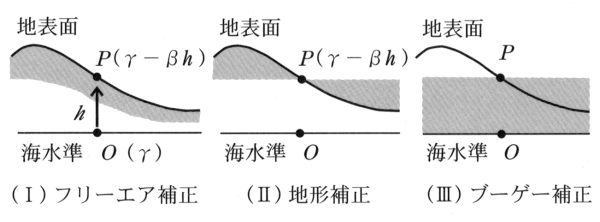
付図2 ブーゲー異常の概念図（駒澤，1998 に加筆修正）

(I) γはO点での正規重力値であるが，フリーエア補正を施すことにより，P点での地球の標準的な 重力値になると考えられる．従って，
　Δg0’ = g - γ + βh = g - (γ - βh)
で与えられるフリーエア異常は，P点での重力値 g と地球の標準モデルである楕 円体の外側にあたるP点での理論重力値(γ-βh)との差である．つまり，フリーエア異常は測点標高 での値であって 海水準での値ではない． ただし，h は測点標高，βは均質地球モデルから得られ る標準的な重力の鉛直勾配である．
(II) P点より高い部分の質量を除去し，低い部分に質量を追加して測定点と同じ 平板状の地形の重力値に補正する（地形補正）．
(III) 標高hの平板状地形の重力効果を除去する（ブーゲー補正）．
(IV) 最終的に，地表面から海水準まで仮定密度ρの効果が除かれて，ブーゲー異常にはρからず れた分の密度構造によるものだけが反映することになる．
　上記の処理をまとめると，ブーゲー異常は次式で表現できる．
　Δg0” = g - γ + (β - 2πGρ)h + ρT + CA
ただし，G は万有引力定数，ρは岩盤の密度(仮定密度) ，ρT は地形補正，CA は大気補正である．

３．表層密度とブーゲー異常の仮定密度の関係
　ブーゲー異常は，仮定密度(もしくは，補正密度)のとり方で地形との相関度が 異なることから，地形が凹凸をもっていれば表層密度の推定ができる．更に，表層の影響を除去した基 盤構造などの深 部構造による成分の抽出に利用される．
　仮定密度の推定の方法としては，(1) 岩石試料の密度測定による方法，(2) 標高 に対して重力の小さくなる割合から推定する方法，(3) ブーゲー異常図と地形図を見比べる方法， が挙げられる． (1) については，岩石のサンプリングは必然的に風化していない状態のものが多 くなり偏りが生ずるので，必ずしも表層密度を反映しているとは限らないが，少なくとも岩石サ ンプルからの密度値は表層密度の上限を与えることになる．(3) については，実際に数種類の仮 定密度のブーゲー異常図を作成し，地形図との相関を目視して地形図との相関の最も小さいものを選べば良い． 付図3に仮定密度によるブーゲー異常のパターン変化の様子を示す．
　仮定密度が大きくなるに従い，ブーゲー異常値が全体的に小さくなっていくのと，地形と正相関 の上に凸から逆相関の下に凸に変化していくのがわかる．地形のパターンと無相関なものが表層 密度（最適な仮定密度）である．

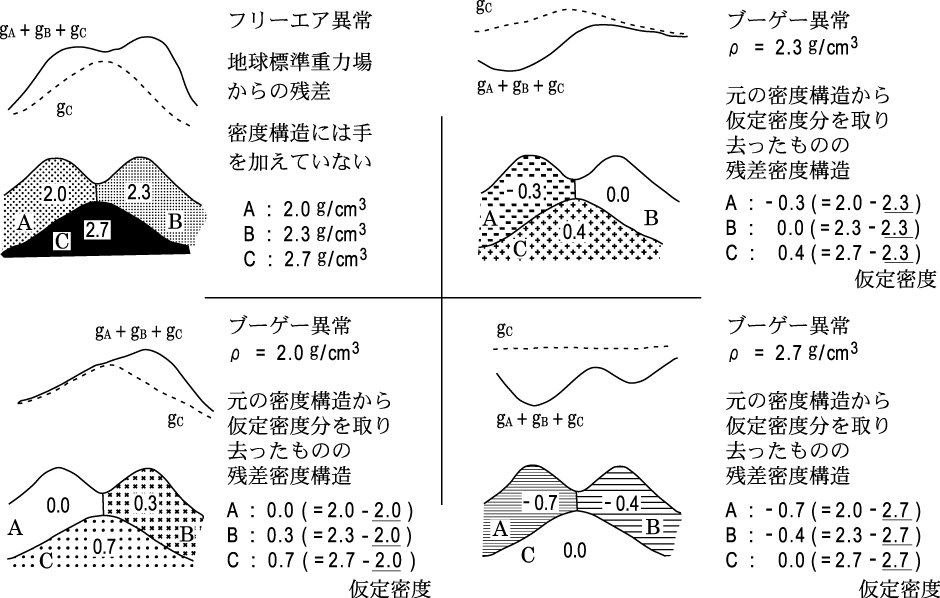
付図3 仮定密度によるブーゲー異常のパターン変化の概念図（駒澤，1998に加筆修正）

４．地質構造に関連する浅部異常の抽出
　フィルターリングは，重力異常や磁気異常から有為な情報を抽出し，定性的な 解析・解釈を進めるのに有効な手法である．重力解析で構造抽出に利用されるものに，大規模・深部構造に対応す る長波長成分を抽出するローパス・フィルター（或いは，ハイカット・フィルター），微細・浅 部構造に対応する短波長成分を抽出するハイパス・フィルター（或いは，ローカット・フィルター） がある．微分フィルターはハイパス・フィルターに含まれる．また，注目する規模・深度に対応し た成分を抽出するバンドパス・フィルターがある．
フィルター操作が最も一般的に使用されるのは，断層等の構造境界の抽出である． 従来，そうした目的には，水平微分(水平勾配)や鉛直2次微分が利用されてきた．水平微分は，直 感的に理解し易いが，微分値の大小で構造や落差の大きさを判断しがちで，深い構造を過小評価 しがちになる． 一方，鉛直2次微分は，深度に関係なく構造境界で値がゼロになる性質がありよく 利用されてきたが，短波長成分がノイズ成分と区別つかなくなるため，線状構造の抽出は難しい 点があった． 一方，鉛直1次微分は過度のハイパス・フィルターにならず，鉛直2次微分ではノイズゾーン （狭域ゾーニング）となっていたところが広域ゾーニング地域となり構造境界が 把握しやすくなることがある．落差が同じで深さが違う簡単な事例を模式的に付図4に示す．段差構造からあ る程度離れると重力差は同じになるが，水平微分を見ると構造が浅い程値が大きくなることわ かる．つまり，構造の深度決定の推定には，微分値が有効であることを示してい る．当然，意味のある水平微分を得るには測点間隔が十分細かく取られていることが必要で ある．

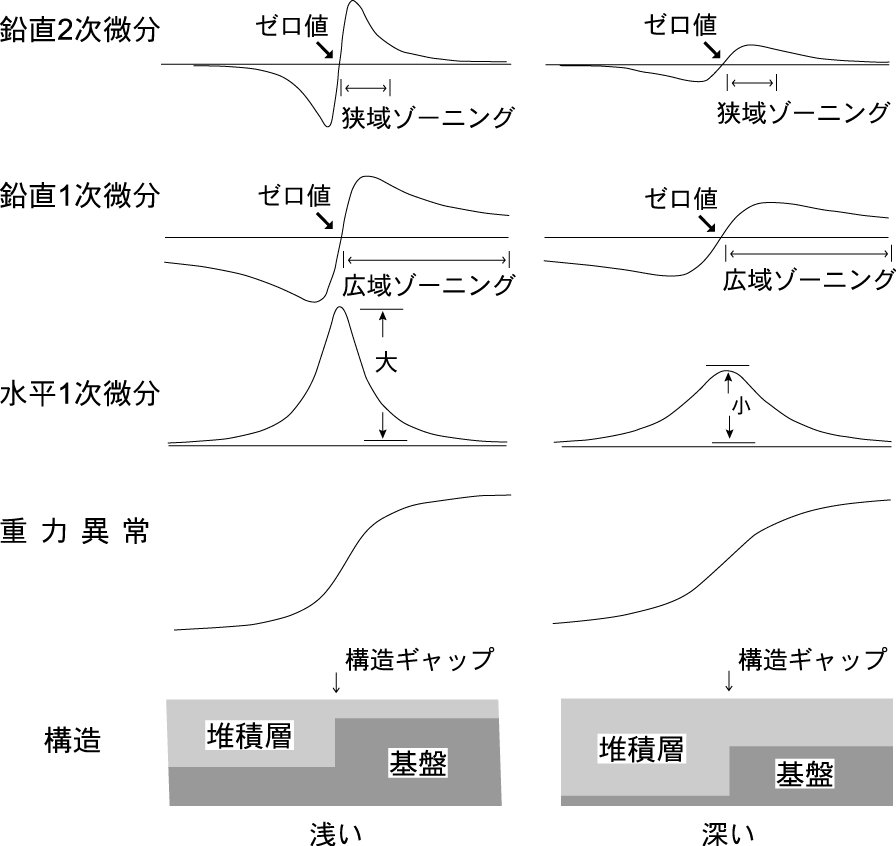
付図4 落差が同じで深さが違う簡単な事例のフィルター図（駒澤，1998に加筆修正）

文献

物理探査学会編 (1989) 図解物理探査, 物理探査学会, 239p.

駒澤正夫 (1998) 物理探査ハンドブック, 手法編第8章, 433-471, 物理探査学会編.